Recently, the group of Prof. WANG Wencheng and HOU Fei in the State Key Laboratory of Computer Sciences, Institute of Software, Chinese Academy of Sciences, developed a new topology-preserving simplification method for Medial Axes in 3D models. Compared with the existing methods, the proposed method has advantages in the geometric approximation accuracy and efficiency, while preserving the topology. Their study entitled "Topology Preserving Simplification of Medial Axes in 3D Models " was presented in the Pacific Conference on Computer Graphics and Applications 2019 and published in Computer Graphics Forum,Vol.37, No.7 2019.
The Medial Axis is an important descriptor of geometry and topology of a 3D model. It has many applications in shape analysis and manipulations. However, the instability to noises of the medial axes makes it necessary simplify the medial axes for further usage. Existing methods have different kinds of drawbacks. Some lack geometric approximation accuracy and some cannot preserve the topology, while some of the others are time-consuming due to topology-check (Figure 1).
The group summarized a novel and simple topology-check strategy for identifying the edges whose collapses could change the topology. With the strategy, the new method can skip the contraction of those edges during the simplification, and thus preserve the topology. Meanwhile, as shown in Figure 2, they proposed to restrict the topology-check in the areas near the holes to avoid much unnecessary topology-checks. Besides, in order to accelerate the whole method, they propose a parallel framework for edge-contraction based simplification. The new method is not only as accurate as the geometric approximation of edge-contraction methods but also much more efficient to preserve the topology.
The research is not only meaningful for the shape understanding and analysis, but also contributes a lot to the widely application of medial axes in other fields. The research is partially supported by the National Natural Science Foundation of China.
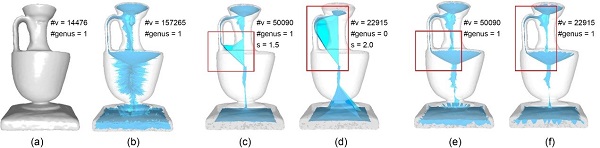
Figure 1: Simplifications of the medial axis of the vase. (a) Original vase model. (b) Initial medial axis. (c)-(d) Simplified medial axes using the SAT method [MGP10] by different scaling parameters s. (e)-(f) Results using our method at correspondingly similar levels of simplification. The number of vertices (#v) and the number of genus (#genus) are described. Our method produces more compact and geometrically accurate results, while the SAT method produces topological errors, as illustrated in the red boxes.(Image by HOU Fei)
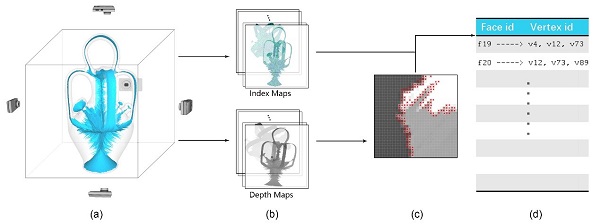
Figure 2: The process of extracting critical areas, where edge-collapse potentially changes the topology. (a)-(b) First, we produce depth maps and corresponding face index maps from 6 different projection directions in viewing the model orthogonally. (b)-(c) Then, we detect pixels with large depth-variance as critical pixels (marked red in (c)) which are likely near the holes. (c)-(d) Finally, we find the corresponding face indices of the critical pixels and label the critical areas consisted of the found faces.(Image by HOU Fei)